Cosine Similarity

Cosine Similarity Explained

To quantify how similar two embedding vectors (and therefore two sentences) are, I used cosine similarity. Cosine similarity measures the cosine of the angle between two vectors. Defined mathematically as:

$\text{Cosine Similarity} = \large \frac{A \cdot B}{\|A\|\|B\|}$

Where:

• $A\cdot B$ denotes the dot product (multiplying corresponding elements and summing).
• $\|A\|$ and $\|B\|$ are the magnitudes (lengths) of vectors A and B.

This is pretty self explanatory when looking at the vectors as, well, vectors. Remember that vectors represent directions in space (one can kind of think of them as arrows). Which means if the angle between these two directions is calculated one can quantify how similar they are based on whether they point in the same direction or not.

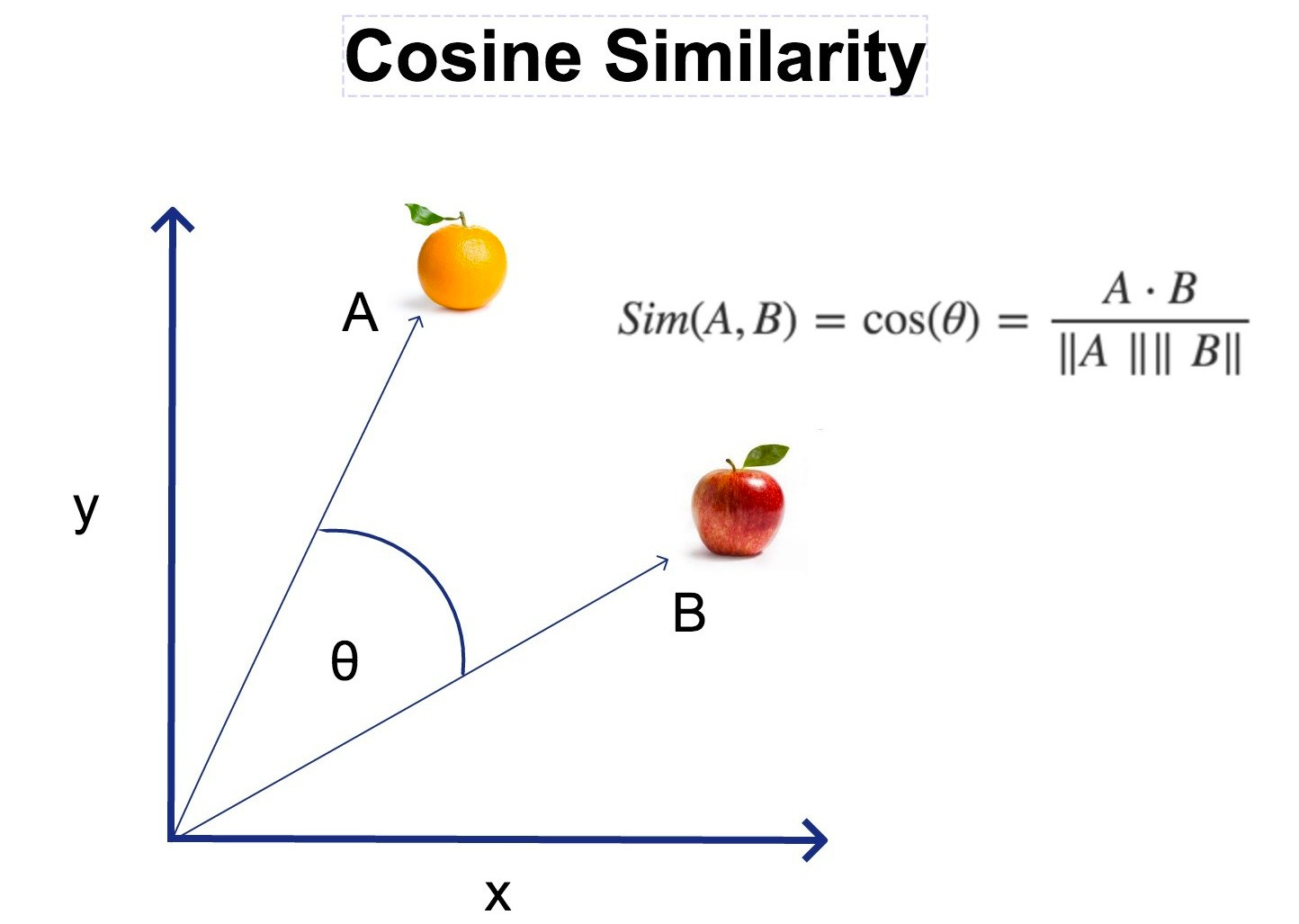Image 3.3 By calculating the angle you can see if these two vectors point in the same direction or not.

The cosine similarity value ranges from -1 (completely opposite) to 1 (identical). A value close to 1 indicates highly similar meaning, whereas values closer to 0 imply unrelated content.

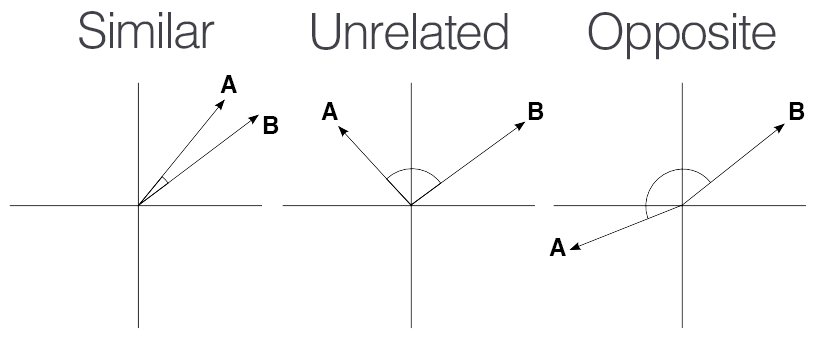Image 3.4 Looking at this in a spacial representation this just means the result is going to be 1 if the vectors are perfectly parallel, 0 if they share a 90 degree angle and -1 if they point in the complete opposite direction.